Bagian 10
SPSS UNTUK PENGUJIAN HIPOTESIS

A. Uji Hipotesis Satu Sampel
Hipotesis adalah pernyataan mengenai sesuatu yang akan dibuktikan kebenarannya lewat penelitian. Untuk menguji hipotesis, langkah pertama yang harus dilakukan adalah merumuskan hipotesis. Rumusan hipotesis tersebut biasanya dinyatakan dalam bentuk hipotesis null dan hipotesis alternatif.
Uji satu sampel untuk rata-rata digunakan untuk menguji rata-rata sampel apakah sesuai dengan rata-rata populasi. Pengujian ini dilakukan untuk memperoleh keyakinan atas nilai rata-rata suatu sampel.

B. Uji Satu Sampel untuk Rata-Rata dengan Aplikasi SPSS
Tahap-tahap pengujian menggunakan program SPSS adalah sebagai berikut:
1. Masukkan data dalam jendela Data View SPSS dengan cara yang sama di mana semua data dikelompokkan dalam satu variabel. Beri nama variabel dengan skor, kemudian isi label dengan Skor TOEFL Mahasiswa.
2.Dari menu Analyze, pilih menu Compare Means, kemudian pilih One-Sampel T Test sehingga keluar jendela berikut.
3. Masukkan variabel skor TOEFL mahasiswa dalam kolom Test Veriable.
4. Abaikan menu yang lain.
5. Klik tombol OK.

C. Uji Hipotesis Dua Sampel
D. Uji t Dua Sampel yang Berpasangan Menggunakan SPSS

Bagian 8

https://docs.google.com/presentation/d/1lx8_Rltlpx9akC74MxHHuJo-nQVXsmT5t6s5Lf-9AOk/edit

Bagian 9
Penggunaan SPSS Untuk Menghitung Validitas dan Reabilitas Data

A. Uji Validitas
Uji validitas dilakukan untuk memastikan seberapa baik suatu instrumen dan untuk mengukur konsep yang harusnya diukur. Sugiyono (2010) untuk menguji validitas dilakukan dengan cara mengkorelasikan antara skor butir pertanyaan dengan skor totalnya.

B. Uji Reabilitas
Suharsimi Arikunto (2006 : 154)
Reabilitas menunjuk pada suatu pengertian bahwa sesuatu instrumen cukup dapat dipercaya untuk digunakan sebagai alat pengumpul data karena instrumen tersebut sudah baik.

C. SPSS (Statistical Product and Service Solution)
merupakan sebuah program aplikasi yang mempunyai kemampuan untuk menganalisis statistik dengan keakuratan yang cukup tinggi.

৹Sejarah SPSS
SPSS dibuat pertama kali pada tahun 1968 oleh tiga mahasiswa Standford University, yaitu Norma H. Nie, C. Hadlai Hull dan Dale H. Bent. Awalnya SPSS diciptakan untuk proses mengolah data dalam Ilmu sosial dengan kepanjangan Statistical Package for the Social Science. Namun sekarang fungsi SPSS sudah diperluas untuk menjalankan berbagai jenis kebutuhan, seperti mengolah produksi barang, hasil reset dll. Singkatan SPSS pun berubah menjadi Statistical Product and Service Solution.

৹Fungsi SPSS
1. Melakukan riset pemasaran (market research)
2. Pengendalian dan perbaikan mutu (quality improvement)
3. Analisis data survey atau kuisioner
4. Banyak digunakan dalam penelitian akademik mahasiswa
5. Banyak digunakan untuk keperluan pemerintah (seperti lembaga BPS)
6. Penelitian kesehatan rakyat dan lain-lain

Bagian 7
Validitas dan Reliabilitas Instrumen Penelitian

Validitas
Ridwan (2016) menyebutkan validitas adalah suatu ukuran yang menunjukan suatu kevalidan dan atau kesahlihan suatu instrumen.

Suatu instrumen yang valid apabila:
1. Mempunya validitas tinggi. Bila validitasnya rendah maka instrumen tersebut kurang valid.
2. Mampu mengukur apa yang hendak diukur atau diinginkan.
3. Dapat mengungkap data dari variabel yang dapat diteliti.

Pengujian validitas internal:
-Pengujian validitas konstruk (constract validity)
Setelah instrumen dikonstruksi tentang aspek-aspek yang akan diukur dengan berlandaskan teori tertentu, maka selanjutnya dikonsultasikan dengan pendapat para ahli (judgment experts). Instrumen yang telah disetujui para ahli tersebut dicoba pada sampel dari mana populasi diambil.

-Validitas isi (content validity)
Dilakukan dengan membandingkan antara isi instrumen dengan materi pelajaran yang telah diajarkan.

-Pengujian validitas eksternal
Validitas eksternal instrumen diuji dengan cara membandingkan antara kriteria yang ada pada instrumen dengan fakta empiris yang terjadi di lapangan. Bila terdapat kesamaan antara kriteria dalam instrumen dengan fakta di lapangan, maka dapat dinyatakan instrumen tersebut mempunya validitas eksternal yang tinggi.

Reliabilitas

Realibilitas menunjuk pada suatu pengertian bahwa suatu instrumen dapat dipercaya untuk digunakan sebagai alat pengumpul data karena instrumen tersebut sudah dianggap baik.
Reliabel juga dipercaya dapat diandalkan. Sehingga beberapa kali di ulang pun hasilnya akan tetap sama (konsisten).

Pengujian reliabilitas secara eksternal:

1. Test-retest
Test-retest dilakukan dengan cara mencoba instrumen beberapa kali pada responden. Jadi dalam hal ini instrumennya sama, respondennya sama, dan waktunya yang berbeda. Reliabilitas diukur dari koefisien korelasi antara percobaan pertama dengan yang berikutnya. Bila koefisien korelasi positif dan signifikan maka instrumen tersebut sudah dinyatakan reliabel.

Contoh:
Akan dilakukan penelitian tentang kemampuan kerja pegaai di PTS. Untuk pengukuran kerja pegawai akan dilakukan instrumen dengan skala Likert. Sebelum instrumen tersebut digunakan untuk pengukuran yang sebenarnya, akan di uji reabilitas terlebih dahulu. Untuk keperluan tersebut peneliti melakukan uji coba instrumen yang sama banyaknya dua kali. Hasil yang diperoleh dari dua kali uji coba tersebut sebagai berikut.


2. Equivalen
Instrumen yang equivalen adalah pertanyaan yang secara bahsa berbeda, tetapi maksudnya sama.
Contoh:
Berapa tahun anda sudah belajar bahasa Korea?
Tahun berapa anda mulai belajar bahasa Korea?

Pengujian reabilitas instrumen dengan cara ini cukup dilakukan sekali, tetapi instrumennya dua, pada responden yang sama, waktu sama, instrumen berbeda. Reliabilitas instrumen dihitung dengan cara mengkorelasikan antara data instrumen yang satu dengan data instrumen yang dijadikan equivalen.

3. Gabungan (test-retest dan equivalen)
Pengujian reliabilitas ini dilakukan dengan cara mencoba dua instrumen yang equivalen beberapa kali ke responden yang sama. Reliabilitas instrumen dilakukan dengan mengkorelasikan dua instrumen, setelah itu dikorelasikan secara silang. Hal ini dapat digambarkan sebagai berikut:

Pengujian reliabilitas secara internal:
Pengujian reliabilitas dengan internal consistency, dilakukan dengan cara mencobakan instrumen sekali saja, kemudian hasil analisis dapat digunakan untuk memprediksi reliabilitas instrumen. Pengujiannya dapat dilakukan dengan teknik belah dua dari Spearman Brown (Split half), KR 20, KR 21, dan Anova Hoyt. Berikut rumus-rumus dan contoh perhitungannya.

1. Rumus Spearman Brown
2. Rumus KR 20 (Kuder Richardson)
3. Rumus KR 21
4. Alda Cronbach
Pengujian reliabilitas dengan teknik Alfa Cronbach dilakukan untuk jenis data interval/essay. Rumus koefisien reliabilitas Alfa Cronbach:

Bagian 6
Populasi dan Sampel

Populasi

Menurut Sugiyono (2017 : 61) Populasi adalah wilayah generalisasi yang terdiri atas : Obyek/subyek yang mempunyai kuantitas dan karakteristik tertentu yang ditetapkan oleh peneliti untk dipelajari dan kemudian ditarik kesimpulannya.

Sedangkan menurut Furqon (2014 :  146) populasi secara formal dapat didedfinisikan sebagai  sekumpulan objek, orang, atau keadaan yang paling tidak memiliki satu karakteristik umum yang sama.

Sampel

Sampel adalah bagian dari jumlah dan karakteristik yang dimiliki oleh populasi. Bila populasi besar, dan peneliti tidak mungkin mempelajari semua yang ada pada populasi, misalnya karena keterbatasan data, tenaga dan waktu, maka peneliti dapat menggunaan sampel yang diambil dari populasi itu (Sugiyono 2017 : 62)

Sedangkan menurut Furqon (2014) secara sederhana sampel berarti bagian dari satu populasi.

Catatan:
Populasi dan sampel umumnya dianggap sebagai kumpulan beberapa individu atau kelompok. Tapi sebenarnya populasi tidak selalau harus terdiri dari lebih dari sastu individu. Seorang individu pun bisa menjadi sebuah populasi. (Sugiyono, 2017 : 62)

Kriteria dan Syarat Pengambilan Sampel

Menurut Sugiyono (2017 : 62) apa yang dipelajari dari sampel, kesimpulannya akan dapat diberlakukan untuk populasi.

Syarat pengambilan sampel adalah populasi harus homogen atau setidaknya memiliki satu karakteristik yang sama. Apabila populasi heterogen, sampel tidak akan representatif (jurnal Unila)

Teknik Sampling

Teknik sampling terbagi dua, yaitu Probability Sampling dan Nonprobability Sampling. Berikut adalah penjelasan tentang teknik sampling menurut Sugiyono (2017  : 63 - 68)

Probability Sampling
- simple random sampling
- proportionate startified random sampling
- disproportionate stratified random sampling
- cluster sampling (area sampling)

Nonprobability Sampling
- sampling sistematis
- sampling kuota
- sampling insidental
- sampling purfosive
- sampling total
- snowball sampling

Menentukan Ukuran Sampel

Rumus untuk menghitung ukuran sampel dan populasi yang tidak diketahui jumlahnya adalah sebagai berikut:
(λ^2  . N. P. Q)/(d^(2 ) (N-1)+ λ^2. P. Q)
Keterangan:
S = jumlah sampel
A² = chi kuadrat yang harganya tergantung derajat kebebasan dan tingkat kesalahan. Untuk derajat kebebasan dan kebebasan 5% harga chi kuadrat = 3,841. Harga chi kuadrat untuk kesalahan 1% = 6,634 dan 10% = 2,706.
N = jumlah populasi
P = peluang benar (0,5)
Q = peluang salah (0,5)
d = perbedaan antara rata-rata sampel dengan rata-rata populasi. Perbedaan bisa 0,01, 0,05, dan 0,10.

Disebutkan dalam Sugiono (2017) Roscoe dalam buku Research Methods For Business (1982 : 253) memberikan saran saran tentang ukuran sampel  untuk penelitian seperti berikut ini.
1. Ukuran sampel yang layak dalam penelitian adalah antara 30 sampai dengan 500
2. Bila sampel dibagi dalam kategori, maka jumlah anggota sampel setiap kategori minimal 30.
3. Bila dalam penelitian akan melakukan analisis multivariate (korelasi atau regresi ganda misalnya) maka jumlah anggota sampel minimal 10 kali dari jumlah variabel ang diteliti. Misalnya variabel penelitiannya ada 5 (independen + dependen), maka jumla anggota sampel = 10 x 5 = 50
4. Untuk penelitian eksperimen yang sederhana, yang menggunakan kelompok eksperimen dan kelompok kontrol makan jumlah anggota sampel masing masing kelompok antara lain 10 s/d 20.

 Bagian 5
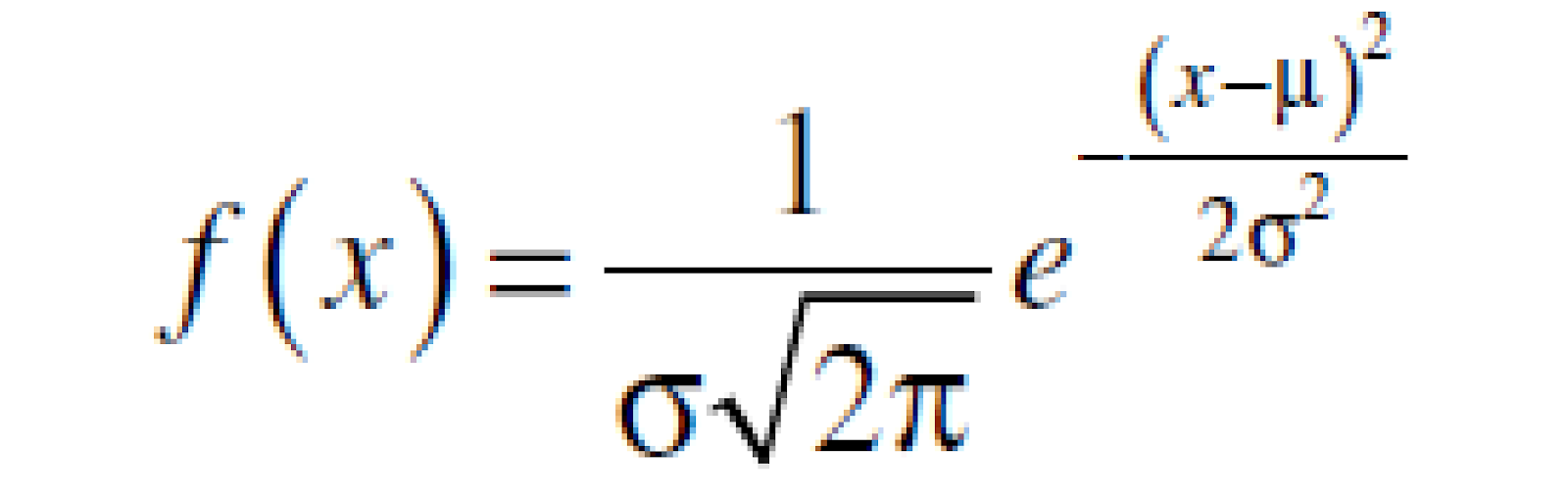
Distribusi Normal dan Standar Deviasi

A. Distribusi Normal
Distribusi Normal atau biasa disebut distribusi gauss adalah salah satu distribusi peluang dengan variable acak kontinu yang paling sering digunakan.

1. Pentingnya Distribusi Normal

• Satu-satunya distribusi probabilitas dengan variabel random kontinu adalah distribusi normal.
• Ada dua peran penting distribusi normal, yaitu :
• Memiliki sifat yang dapat dijadikan satu patokan dalam pengambilan kesimpulan dari beberapa sampel
• Distribusi normal terjadi secara alamiah, banyak peristiwa di dunia nyata yang terdistribusisecara normal.

Fungsi kerapatan probabilitas dari distribusi normal diberikan dalam rumus berikut:

• π =nilai konstan yang ditulis hingga empat desimal (3,1416)
• e = bilangan konstan, bila ditulis hingga empat desimal  e = 2,7183
• µ = parameter, merupakan rata-rata untuk distribusi
• σ = parameter, merupakan simpangan baku untuk distribusi.

Dan nilai x punya batas -∞ < x < ∞, maka dikatakan bahwa variabel acak x berdistribusi normal.

2. Kurva Distribusi Normal

Jika σ makin besar, kurvanya semakin rendah (platikurtik) dan untuk σ makin kecil kurvanya semakin tinggi (leptokurtik).

3. Ciri Distribusi Normal

• Nilai peluang peubah acak dalam distribusi peluang normal dinyatakan dalam luas dari dibawah kurva berbentuk genta atau lonceng (bell shaped curve).
• Kurva maupun persamaan normal melibatkan  nilai x, µ, dan σ.
• Keseluruhan kurva yang bernilai 1 akan menggambarkan sifat peluang yang tidak pernah negatif dan maksimal bernilai 1.

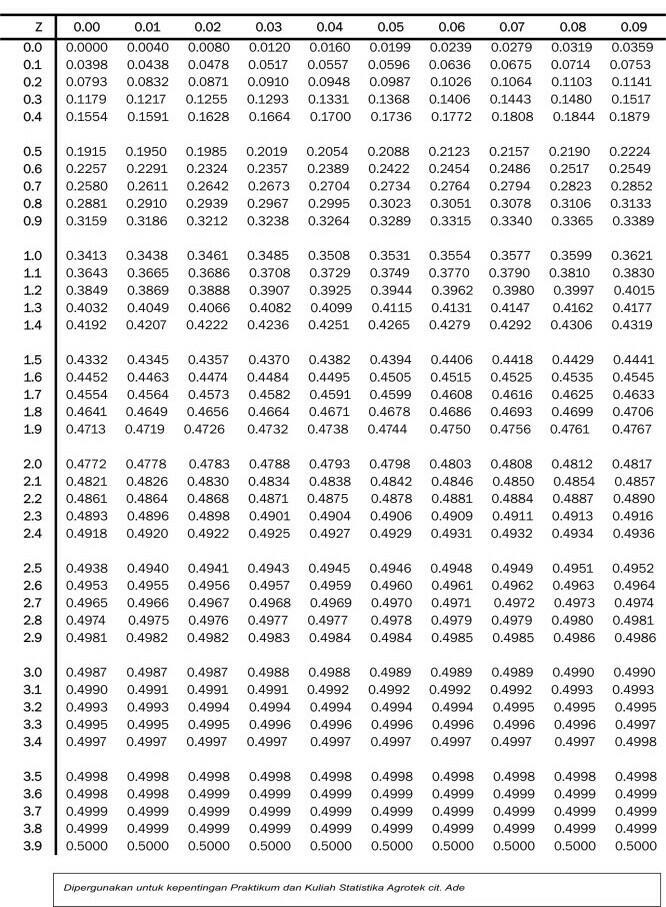
4. Menentukan Luas Daerah dengan Menggunakan Tabel Z

1. Menghitung nilai Z sampai dua desimal.
2. Menggambar kurva normal standar.
3. Meletakkan nilai Z pada sumbu x kemudian menarik garis vertikal yang memotong kurva
4. Nilai yang terdapat dalam daftar merupakan luas daerah antar garis tersebut dengan garis vertikal dititik 0
5. Dalam daftar distribusi normal standar mencari tempat harga Z pada kolom paling kiri hanya sampai satu desimal dan mencari desimal kedua pada baris paling atas
6. Dari Z ke kolom kiri maju ke kanan dan dari Z dibaris atau turun ke bawah, sehingga didapat bilangan yang merupakan luas daerah yang dicari.

Contoh:

1. Panjang roti yang diproduksi suatu pabrik berdistribusi normal dengan rata-rata 25cm dan simpangan baku 2cm. Berapa persen roti yang diproduksi dengan panjang kurang dari 23cm. Dalam soal disamping, µ = 25cm, σ = 2cm. Jika X meyatakan panjang roti yang diproduksi pabrik tersebut, soal ini menanyakan P[x < 23cm]. Yang ditanyakan ini dapat digambarkan sebagai berikut.

5. Ukuran Penyebaran

• Dispersi terdiri atas =
• Jangkauan
• Jangkauan antar kuartil
• Simpangan kuartil

6. Jangkauan/Rentang

Jangkauan atau rentang atau range adalah ukuran dispersi yang paling mudah ditentukan. 

• J = Xmax – Xmin

• J = jangkauan/rentang/range
• Xmax = nilai tertinggi dari data
• Xmin = nilai terendah dari data

Contoh:

• DATA TUNGGAL

1. Diketahui data sebagai berikut :

3, 2, 3, 5, 5, 18, 10.Tentukan rangenya!

Jawab :

J = Xmax – Xmin

= 18 – 2

= 16 

7. Jangkuan Antar Kuartil/Hamparan (H)

Jangkauan antar kuartil atau biasa disebut hamparan merukapan selisih dari kuartil 3 dan kuartil 1.

• 
  JAK = H

= K3 – K1

Contoh:

• DATA TUNGGAL

1. Diketahui data sebagai berikut :

6, 2, 3, 8, 9, 19, 11.Tentukan jangkauan antar kuartilnya!

Jawab :

Urutan data = 2, 3 (K1), 6, 8(K2), 9, 11(K3), 19.

JAK = K3 – K1

= 11– 3

= 8

8. Simpangan Kuartil (Qd)

Simpangan kuartil atau jangkauan semi antar kuartil adalah setengah dari jangkauan antar kuartil.

9. Simpangan Rata-rata (Deviasi Rata-rata) 

Simpangan rata-rata atau deviasi rata-rata adalah suatu simpangan nilai tiap datum terhadap rataan hitungnya. 

B. Standar Deviasi

• Standar deviasi atau simpangan baku adalah salah satu teknik statistic yang lazim digunakan untuk menjelaskan homogenesitas kelompok.
• Standar deviasi merupakan nilai statistik yang biasa digunakan untuk menentukan bagaimana sebaran data dalam sampel, serta seberapa dekat titik data individu ke mean atau rata-rata nilai sampel.

Fungsi Standar Deviasi

Standar deviasi umumnya dipakai oleh para ahli statistic atau orang yang terjun di dunia statistic untuk mengetahui apakah sampel data yang diambil mewakili seluruh populasi. Mencari data yang tepat untuk suatu populasi sangat sulit untuk dilakukan. Oleh karena itu dipakai sampel data yang mewakili seluruh populasi. Hal ini akan memudahkan seseorang untuk melakukan penelitian.

Bagian 4
Kuartil, Desil, dan Persentil

1. Kuartil

a. Pengertian
Beberapa kumpulan data yang sudah diurutkan dari data terkecil hingga data terbesar atau sebaliknya yang kemudian dibagi menjadi empat bagian yang sama banyak.
Kuartil dibagi menjadi tiga macam yaitu K1, K2, K3. Pemberian nama ini ditentukan dari nilai kuartil yang paling kecil. (Andi, 2007)

b. Macam-macam Kuartil

-Kuartil Data Tunggal
1. Menyusun data dimulai dari data terkecil hingga data terbesar.
2. Menentukan letak kuartil yang diminta dengan menggunakan rumus

-Kuartil Dara Kelompok

2. Desil

Nilai atau angka yang membagi data yang menjadi 10 bagian yang sama, setelah disusun dari data terkecil hingga data terbesar atau sebaliknya. Dan desil hanya memiliki 9 nilai. Ada 2 (dua) kelompok desil. Yaitu nilai data desil yang belum dikelompokan (data tunggal) dan nilai data desil yang sudah

dikelompokkan (data berkelompok).

-Desil Data Tunggal

Dn = desil ke –

n = jumlah data

i = urutan desil

-Desil Data Berkelompok

3. Persentil

Nilai yang membagi data menjadi 100 bagian yang sama. Setelah disusun dari angka terkecil sampai ke yang terbesar. Harga persentil ada 99 bagian yaitu Ps1, Ps2, Ps3, ......., Ps99.

-Persentil Data Tunggal

Keterangan:
Pi = persentil ke-
n = jumlah data

i = urutan persentil

-Persentil Data Berkelompok

b = tepi bawah kelas interval
p = panjang kelas interval
i = letak Psi
n = banyak data
Fk = frekuensi kumulatif sebelum kelas Psi
f = frekuensi kelas Psi